Call:
lm(formula = mpg ~ hp + wt)
Residuals:
Min 1Q Median 3Q Max
-3.941 -1.600 -0.182 1.050 5.854
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.22727 1.59879 23.285 < 2e-16 ***
hp -0.03177 0.00903 -3.519 0.00145 **
wt -3.87783 0.63273 -6.129 1.12e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.593 on 29 degrees of freedom
Multiple R-squared: 0.8268, Adjusted R-squared: 0.8148
F-statistic: 69.21 on 2 and 29 DF, p-value: 9.109e-12Stats:
Multiple Linear Regression;
Logistic Regression
2024-10-29
Week TEN
New Logo
from Lego Batman

Homework
Everyone did the homework correctly except that one student submitted the wrong assignment. I thought some people would be thrown off by the different column names in destination airports in two different data frames (faa and dest) but that was not the case.
Multiple Linear Regression
Multiple regression intro (Chapter 9)
Everything we’ve done so far has assumed that we know one piece of information’s relationship to another piece of information. Take the example of teams, where we knew the payroll and want to know the number of wins. Suppose we also knew a number of other statistics that might affect wins. How would we incorporate them? The answer is simple. We add them.
Because we’re using a linear equation, that is, the equation of a line to model the data, there’s no reason we can’t add terms to the equation. These terms are additive, meaning that we add each term and each term has a coefficient. So now, our estimate of \(y\), which we call \(\hat{y}\), looks like this for \(n\) terms.
\[\hat{y}=b_0+b_1x_1+b_2x_2+\cdots+b_nx_n\]
In R, we simply add the column names. For example, consider the built-in data frame mtcars where the outcome variable is mpg. We can construct a model of the relationship between mpg and two input variables we suspect of influencing mpg as follows.
The output looks a bit different now. First, there are 32 residuals, so the individual residuals are not listed. Instead, you see summary statistics for the residuals.
Next, look at the coefficients table. There are three rows now, for the intercept, for hp, and for wt. Notice that all three have significance codes at the end of the row. Normally, you shouldn’t be concerned about the significance code for the intercept, but the other two are interesting. The code for hp is two stars, meaning that it is less than 0.01, while the code for wt is three stars, meaning that it is less than 0.001. The \(p\)-value of 1.12e-06, which is abbreviated scientific notation, means to take 1.12 and shift the decimal point six places to the left, giving 0.00000112 as the decimal equivalent.
The residual standard error is 2.593 on 29 degrees of freedom. As mentioned before, the residual standard error (often abbreviated \(R\!S\!E\)) is the square root of the expression formed by the ratio of the residual sum of squares (often abbreviated \(R\!S\!S\)) divided by the degrees of freedom. Expressing this as a formula is as follows.
\[R\!S\!E=\sqrt{\frac{R\!S\!S}{\text{df}}}\]
\(R\!S\!S\) can be found in R for the above model as follows.
Similarly, \(R\!S\!E\) can be found in R for the above model as follows.
The mathematical formulas for these values are as follows.
\[\begin{align*} R\!S\!S&=\sum_{i=1}^{n}(y_i-\hat{y}_{i})^2 \\ &=S\!S_{yy}-\hat{\beta}_1S\!S_{xy} \end{align*}\]
The term \(S\!S_{xy}\) in the preceding formula is only relevant for simple linear regression with one predictor, where \(S\!S_{xy}= \sum(x_i-\overline{x})(y_i-\overline{y})\). A formula for \(\hat{\beta}_1\) in that case would be the following.
\[\hat{\beta}_1=\frac{S\!S_{xy}}{S\!S_{xx}}\]
\(S\!S_{xx}\) in that case would be the sum of squares of deviations of the predictors from their mean: \(\sum(x_i-\overline{x})^2\).
\[R\!S\!E=\sqrt{\frac{\sum_{i=1}^{n}(y_i-\hat{y}_{i})^2}{n-(k+1)}} \]
where \(k\) is the number of parameters being estimated. For example, in the above model wt and hp are the two parameters being estimated.
The Multiple R-squared is 82 percent and the Adjusted R-squared is 81 percent. This is a good sign because the Adjusted R-squared is adjusted for the case where you have included too many variables on the right hand side of the linear model formula. If it’s similar to Multiple R-squared, that means you probably have not included too many variables.
\[ R^2=\frac{S\!S_{yy}-R\!S\!S}{S\!S_{yy}} =1-\frac{R\!S\!S}{S\!S_{yy}} \]
\[ R^2_a=1-\left(\frac{n-1}{n-(k+1)}\right)(1-R^2) \]
The \(F\)-statistic is important now, because of its interpretation. The \(F\)-statistic tells you that at least one of the variables is significant, taken in combination with the others. The \(t\)-statistics only give the individual contribution of the variables, so it’s possible to have a significant \(t\)-statistic without a significant \(F\)-statistic. The first thing to check in regression output is the \(F\)-statistic. If it’s too small, i.e., has a large \(p\)-value, try a different model.
\[F_c=\frac{(S\!S_{yy}-R\!S\!S)/k}{R\!S\!S/[n-(k+1)]} =\frac{R^2/k}{(1-R^2)/[n-(k+1)]}\]
The \(c\) subscript after \(F\) simply signifies that it is the computed value of \(F\), the one you see in the regression table. This is to contrast it with \(F_\alpha\), the value to which you compare it in making the hypothesis that one or more variables in the model are significant. You don’t need to compute \(F_\alpha\) since the \(p\)-value associated with \(F_c\) gives you enough information to reject or fail to reject the null hypothesis that none of the variables in the model are significant. If you want to calculate it anyway, you can say the following in R:
The preceding calculation assumes you choose 0.05 as the alpha level and that there are \(k=2\) parameters estimated in the model and that \(n-(k+1)=29\). These are the numerator and denominator degrees of freedom.
You might think that including more variables results in a strictly better model. This is not true for reasons to be explored later. For now, try including all the variables in the data frame by the shorthand of a dot on the right hand side of the formula.
Call:
lm(formula = mpg ~ ., data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.4506 -1.6044 -0.1196 1.2193 4.6271
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.30337 18.71788 0.657 0.5181
cyl -0.11144 1.04502 -0.107 0.9161
disp 0.01334 0.01786 0.747 0.4635
hp -0.02148 0.02177 -0.987 0.3350
drat 0.78711 1.63537 0.481 0.6353
wt -3.71530 1.89441 -1.961 0.0633 .
qsec 0.82104 0.73084 1.123 0.2739
vs 0.31776 2.10451 0.151 0.8814
am 2.52023 2.05665 1.225 0.2340
gear 0.65541 1.49326 0.439 0.6652
carb -0.19942 0.82875 -0.241 0.8122
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.65 on 21 degrees of freedom
Multiple R-squared: 0.869, Adjusted R-squared: 0.8066
F-statistic: 13.93 on 10 and 21 DF, p-value: 3.793e-07You might find this output a bit surprising. You know from the \(F\)-statistic that at least one of the variables is contributing significantly to the model but individually, the contributions seem minimal based on the small \(t\)-statistics. The model is only a bit better, explaining 86 percent of the variability in the data, and the adjusted \(R^2\) value hasn’t improved at all, suggesting that you may have too many variables.
At this stage, you would probably remove some variables, perhaps by trial and error. How would you do this? You could start by running linear models over and over again. For example, you could construct one linear model for each variable and see which one has the largest contribution. Then you could try adding a second variable from among the remaining variables, and do that with each remaining variable, until you find one that adds the Largest contribution. You could continue in this way until you’ve accounted for all the variables, but would take forever to do.
Luckily, R has functions to assist with this process and run regressions for you over and over again. I’m going to demonstrate one of them now for which we have to add the leaps package. I should point out that this involves doing some machine learning which is not strictly in the scope of this class, but will save you a lot of time.
pacman::p_load(caret)
pacman::p_load(leaps)
set.seed(123)
train.control <- trainControl(method = "cv", number = 10)
m <- train(mpg ~ ., data = mtcars,
method = "leapBackward",
tuneGrid = data.frame(nvmax = 1:10),
trControl = train.control
)
m$results nvmax RMSE Rsquared MAE RMSESD RsquaredSD MAESD
1 1 3.528852 0.8077208 3.015705 1.765926 0.2320177 1.529370
2 2 3.104015 0.8306301 2.507496 1.355870 0.2108183 0.884356
3 3 3.211552 0.8255871 2.700867 1.359334 0.2077318 1.033360
4 4 3.148479 0.8296845 2.630645 1.354017 0.1908016 1.074414
5 5 3.254928 0.8164973 2.737739 1.266874 0.2309531 1.044970
6 6 3.259540 0.8212797 2.749594 1.227337 0.2493678 1.043727
7 7 3.322310 0.8570599 2.787698 1.408879 0.1592820 1.153164
8 8 3.297613 0.8666992 2.744000 1.364396 0.1529011 1.114000
9 9 3.330123 0.8632282 2.751539 1.385199 0.1600841 1.111120
10 10 3.286242 0.8588116 2.715828 1.362054 0.1739366 1.120088[1] 2Subset selection object
10 Variables (and intercept)
Forced in Forced out
cyl FALSE FALSE
disp FALSE FALSE
hp FALSE FALSE
drat FALSE FALSE
wt FALSE FALSE
qsec FALSE FALSE
vs FALSE FALSE
am FALSE FALSE
gear FALSE FALSE
carb FALSE FALSE
1 subsets of each size up to 2
Selection Algorithm: backward
cyl disp hp drat wt qsec vs am gear carb
1 ( 1 ) " " " " " " " " "*" " " " " " " " " " "
2 ( 1 ) " " " " " " " " "*" "*" " " " " " " " " (Intercept) wt qsec
19.746223 -5.047982 0.929198
Call:
lm(formula = mpg ~ wt + qsec, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-4.3962 -2.1431 -0.2129 1.4915 5.7486
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.7462 5.2521 3.760 0.000765 ***
wt -5.0480 0.4840 -10.430 2.52e-11 ***
qsec 0.9292 0.2650 3.506 0.001500 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.596 on 29 degrees of freedom
Multiple R-squared: 0.8264, Adjusted R-squared: 0.8144
F-statistic: 69.03 on 2 and 29 DF, p-value: 9.395e-12The preceding code uses a process of backward selection of models and arrives at a best model with two variables. Backward selection starts with all the variables and gradually removes the worst one at each iteration.
The following code uses a process of sequential selection, which combines both forward and backward. It takes longer to run, but can result in a better model. In this case, it chooses four variables.
m <- train(mpg ~ ., data = mtcars,
method = "leapSeq",
tuneGrid = data.frame(nvmax = 1:10),
trControl = train.control
)
m$results nvmax RMSE Rsquared MAE RMSESD RsquaredSD MAESD
1 1 3.338459 0.9001241 2.890096 1.0951033 0.1013687 0.9516300
2 2 3.189923 0.8859776 2.582903 0.6838624 0.1267838 0.4331819
3 3 2.941144 0.8620702 2.488212 0.9202376 0.1449517 0.6399695
4 4 2.879207 0.8617366 2.480590 1.0315877 0.1534301 0.8871564
5 5 3.132200 0.8965810 2.747981 1.0959380 0.1336679 0.9911532
6 6 3.010670 0.9150866 2.656875 1.0023198 0.1083813 0.8800647
7 7 2.919346 0.9260098 2.499461 0.8913467 0.1133718 0.7935931
8 8 2.985337 0.9085432 2.585924 0.9516997 0.1248117 0.8376843
9 9 3.022897 0.9194308 2.609043 1.1395931 0.1111588 1.0913428
10 10 3.257194 0.8988626 2.811998 1.3089386 0.1423077 1.2115681[1] 4Subset selection object
10 Variables (and intercept)
Forced in Forced out
cyl FALSE FALSE
disp FALSE FALSE
hp FALSE FALSE
drat FALSE FALSE
wt FALSE FALSE
qsec FALSE FALSE
vs FALSE FALSE
am FALSE FALSE
gear FALSE FALSE
carb FALSE FALSE
1 subsets of each size up to 4
Selection Algorithm: 'sequential replacement'
cyl disp hp drat wt qsec vs am gear carb
1 ( 1 ) " " " " " " " " "*" " " " " " " " " " "
2 ( 1 ) "*" "*" " " " " " " " " " " " " " " " "
3 ( 1 ) "*" " " "*" " " "*" " " " " " " " " " "
4 ( 1 ) " " " " "*" " " "*" "*" " " "*" " " " " (Intercept) hp wt qsec am
17.44019110 -0.01764654 -3.23809682 0.81060254 2.92550394
Call:
lm(formula = mpg ~ hp + wt + qsec + am, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.4975 -1.5902 -0.1122 1.1795 4.5404
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17.44019 9.31887 1.871 0.07215 .
hp -0.01765 0.01415 -1.247 0.22309
wt -3.23810 0.88990 -3.639 0.00114 **
qsec 0.81060 0.43887 1.847 0.07573 .
am 2.92550 1.39715 2.094 0.04579 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.435 on 27 degrees of freedom
Multiple R-squared: 0.8579, Adjusted R-squared: 0.8368
F-statistic: 40.74 on 4 and 27 DF, p-value: 4.589e-11Which model is better? The latter model has the best adjusted \(R^2\) value. But it also has what appears to be a spurious variable, hp. It could be that hp is contributing indirectly, by being collinear with one of the other variables. Should we take it out and try again or should we accept the two variable model? That depends on several factors.
There is a principle called Occam’s Razor, named after William of Occam (who didn’t invent it, by the way—things often get named after popularizers rather than inventors). The principle states that, if two explanations have the same explanatory power, you should accept the simpler one. In this context, simpler means fewer variables. The tricky part is what is meant by the same explanatory power. Here we have a comparison of 0.8368 adjusted \(R^2\) vs 0.8144. Are those close enough to be considered the same? It depends on the context.
If you’re a car buyer I would say yes but if you’re a car manufacturer I would say no. Your opinion might differ. It’s easy to teach the mechanics of these methods (even if you don’t think so yet!) but much harder to come up with the insights to interpret them. (Actually, I would probably choose the three variable model of wt, qsec, and am, but you can test that for yourself.)
Feature selection with qualitative variables
Unfortunately, the leaps package is not much help with qualitative variables. Another approach is to use the olsrr package as follows.
pacman::p_load(olsrr)
m <- lm(price ~ carat + cut + color + clarity, data = diamonds)
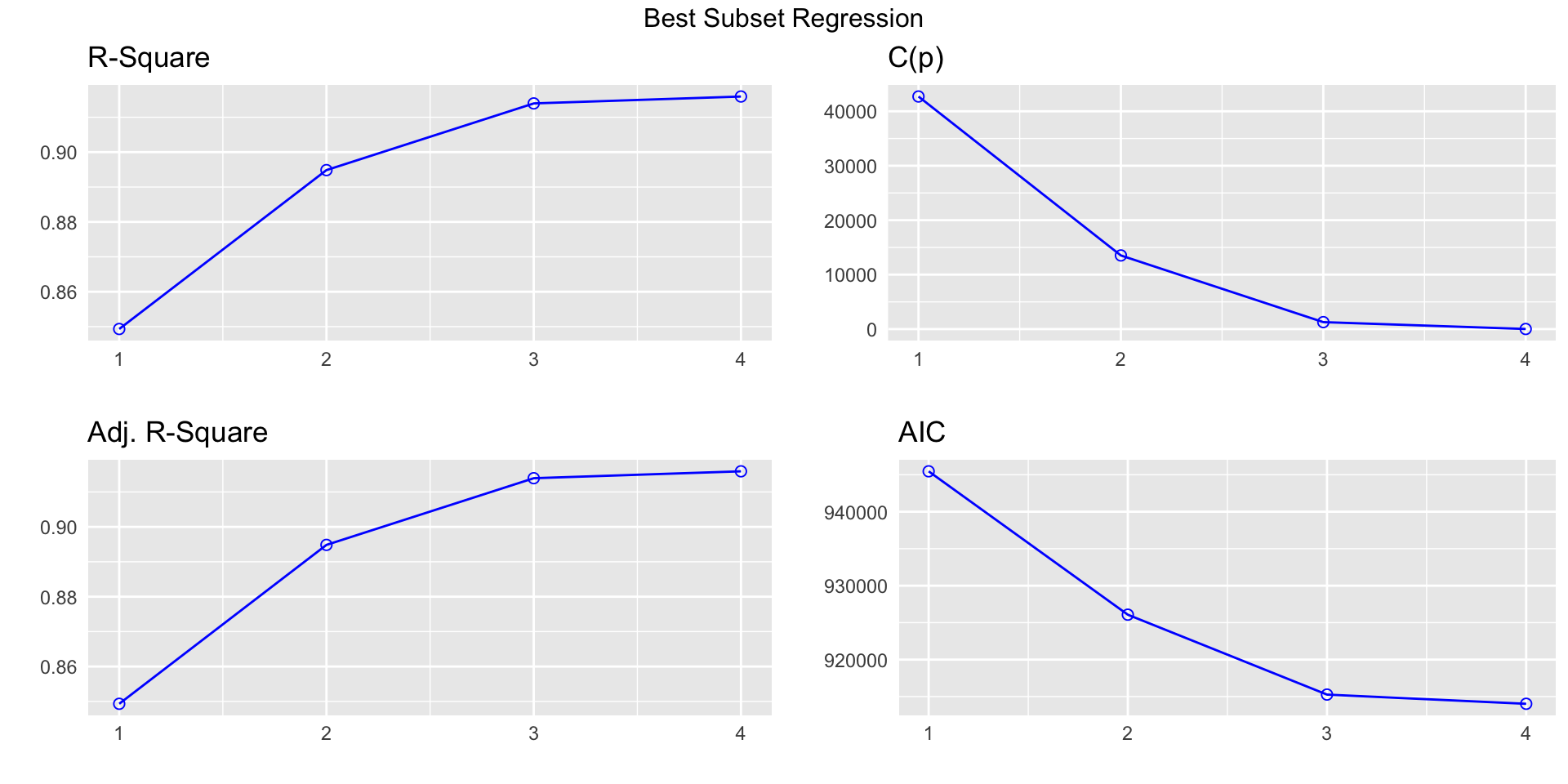
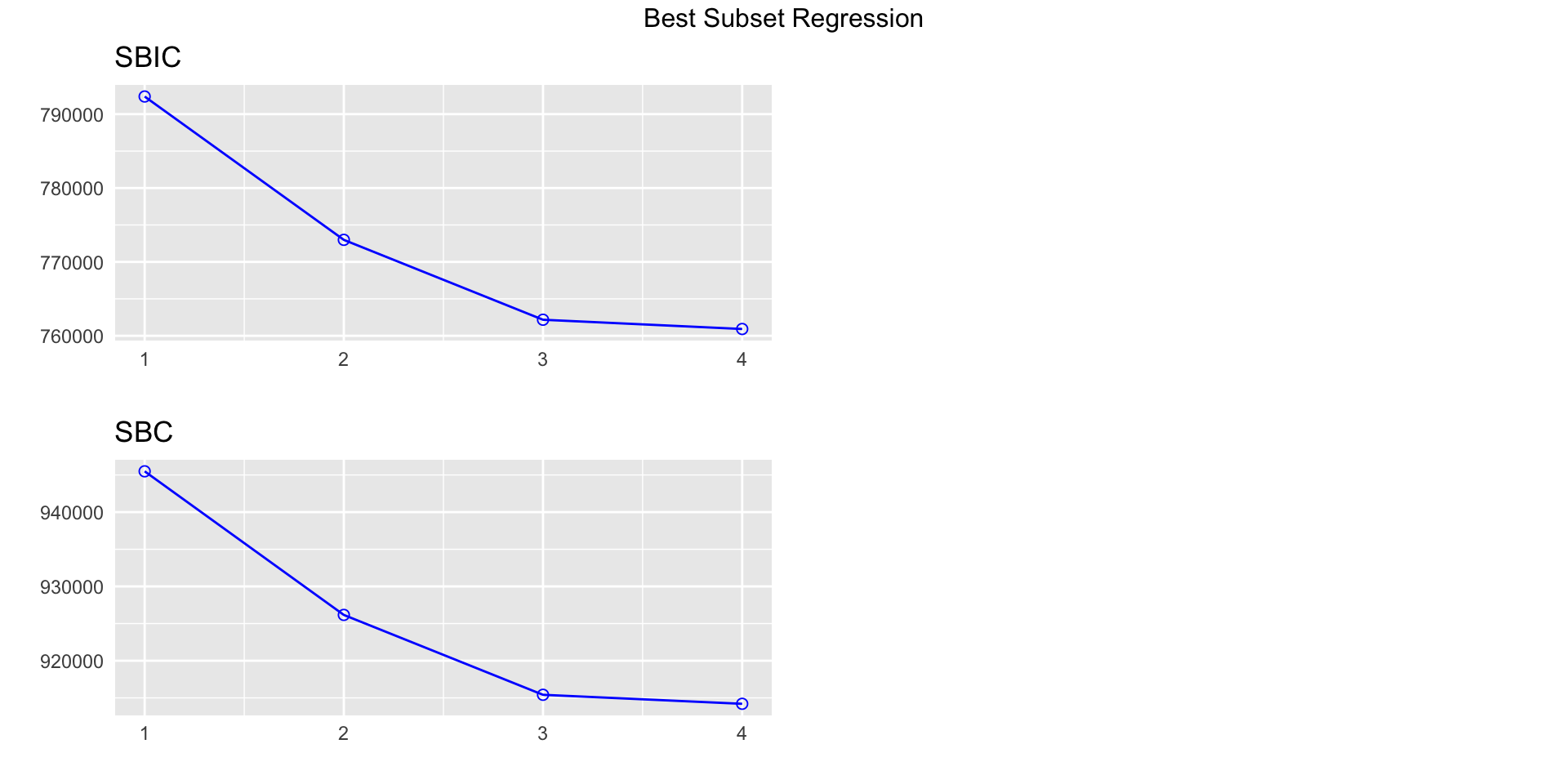
k <- ols_step_best_subset(m)
k Best Subsets Regression
--------------------------------------
Model Index Predictors
--------------------------------------
1 carat
2 carat clarity
3 carat color clarity
4 carat cut color clarity
--------------------------------------
Subsets Regression Summary
--------------------------------------------------------------------------------------------------------------------------------------------------------------
Adj. Pred
Model R-Square R-Square R-Square C(p) AIC SBIC SBC MSEP FPE HSP APC
--------------------------------------------------------------------------------------------------------------------------------------------------------------
1 0.8493 0.8493 0.8493 42712.8488 945466.5323 792389.2852 945493.2192 129350491485.6152 2398132.8805 44.4601 0.1507
2 0.8949 0.8948 0.8948 13524.4373 926075.5885 772987.2178 926164.5448 90268965134.5953 1673786.2236 31.0311 0.1052
3 0.9140 0.9139 0.9139 1280.6557 915270.4554 762173.1841 915412.7855 73867441333.4426 1369818.0969 25.3957 0.0861
4 0.9159 0.9159 0.9159 19.0000 914023.0749 760919.9895 914200.9875 72169466027.5527 1338429.6533 24.8138 0.0841
--------------------------------------------------------------------------------------------------------------------------------------------------------------
AIC: Akaike Information Criteria
SBIC: Sawa's Bayesian Information Criteria
SBC: Schwarz Bayesian Criteria
MSEP: Estimated error of prediction, assuming multivariate normality
FPE: Final Prediction Error
HSP: Hocking's Sp
APC: Amemiya Prediction Criteria Note on ordered factors
When you conduct a linear regression, you are generally looking for the linear effects of input variables on output variables. For example, consider the diamonds data frame that is automatically installed with ggplot. The price output variable may be influenced by a number of input variables, such as cut, carat, and color. It happens that R interprets two of these as ordered factors and does something interesting with them. Let’s conduct a regression of price on cut.
Call:
lm(formula = price ~ cut, data = diamonds)
Residuals:
Min 1Q Median 3Q Max
-4258 -2741 -1494 1360 15348
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4062.24 25.40 159.923 < 2e-16 ***
cut.L -362.73 68.04 -5.331 9.8e-08 ***
cut.Q -225.58 60.65 -3.719 2e-04 ***
cut.C -699.50 52.78 -13.253 < 2e-16 ***
cut^4 -280.36 42.56 -6.588 4.5e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3964 on 53935 degrees of freedom
Multiple R-squared: 0.01286, Adjusted R-squared: 0.01279
F-statistic: 175.7 on 4 and 53935 DF, p-value: < 2.2e-16Note that the output includes four independent variables instead of just cut. The first one, cut.L, represents cut. The L stands for linear and estimates the linear effect of cut on price. The other three are completely independent of the linear effect of cut on price. The next, cut.Q, estimates the quadratic effect of cut on price. The third, cut.C, estimates the cubic effect of cut on price. The fourth, cut^4 estimates the effect of a fourth degree polynomial contrast of cut on price. Together, all four of these terms are orthogonal polynomial contrasts. They are chosen by R to be independent of each other since a mixture could reveal spurious effects. Why did R stop at four such contrasts? Let’s examine cut further.
You can see that cut has five levels. R automatically chooses \(\text{level}-1\) polynomial contrasts when presented with an ordered factor. How can you make R stop doing this if you don’t care about the nonlinear effects? You can present the factor as unordered without altering the factor as it is stored. Then your regression output will list one term for each level of the factor, estimating the effect of that level on the output variable.
Call:
lm(formula = price ~ cut, data = diamonds)
Residuals:
Min 1Q Median 3Q Max
-4258 -2741 -1494 1360 15348
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4358.76 98.79 44.122 < 2e-16 ***
cutGood -429.89 113.85 -3.776 0.000160 ***
cutVery Good -377.00 105.16 -3.585 0.000338 ***
cutPremium 225.50 104.40 2.160 0.030772 *
cutIdeal -901.22 102.41 -8.800 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3964 on 53935 degrees of freedom
Multiple R-squared: 0.01286, Adjusted R-squared: 0.01279
F-statistic: 175.7 on 4 and 53935 DF, p-value: < 2.2e-16By the way, you can also say it in one line as:
Call:
lm(formula = price ~ factor(cut, ordered = F), data = diamonds)
Residuals:
Min 1Q Median 3Q Max
-4258 -2741 -1494 1360 15348
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4358.76 98.79 44.122 < 2e-16 ***
factor(cut, ordered = F)Good -429.89 113.85 -3.776 0.000160 ***
factor(cut, ordered = F)Very Good -377.00 105.16 -3.585 0.000338 ***
factor(cut, ordered = F)Premium 225.50 104.40 2.160 0.030772 *
factor(cut, ordered = F)Ideal -901.22 102.41 -8.800 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3964 on 53935 degrees of freedom
Multiple R-squared: 0.01286, Adjusted R-squared: 0.01279
F-statistic: 175.7 on 4 and 53935 DF, p-value: < 2.2e-16Notice that generating the orthogonal polynomial contrasts does not alter the linear model in any way. It’s just extra information. Both models produce the same \(R^2\) and the same \(F\)-statistic and the same \(p\)-value of the \(F\)-statistic.
It is VERY important to note that there is an assumption in the generation of these orthogonal polynomial contrasts. They assume that the differences between the levels of the ordered factor are evenly spaced. If the levels are not evenly spaced, the information provided will be misleading. Take for instance the world’s top three female sprinters. I read an article claiming that the difference between the top two (Richardson and Jackson at the time of this writing) was much smaller than the difference between the second and third. There are many statistical tools that use ranks, such as 1, 2, and 3, as ordered factors. Here is a case where that would be misleading.
How can you use this information? In a basic course like this, the information is not particularly useful and we will not pursue it. If you go on in statistics or data science, you will soon encounter situations where nonlinear effects matter a great deal.
For example, this often arises in age-period-cohort analysis, where you want to separate the effects of people’s ages, usually divided into evenly spaced levels, and other numerical factors such as income, also usually divided into evenly spaced levels, and the effects of significant periods, such as the economic collapse of 2008 or the pandemic beginning in 2019, and finally the effects of being a member of a cohort or identifiable group. This kind of analysis is often conducted by epidemiologists, people with very large groups of customers, policymakers, and others concerned with large groups of people, or any “objects” with large numbers of attributes.
More on Multiple regression
The OpenIntro Stats book gives an example of multiple regression with the mariokart data frame from their website. This involves the sale of 143 copies of the game Mario Kart for the Wii platform on eBay. They first predict the price based on most of the variables, like so.
load(paste0(Sys.getenv("STATS_DATA_DIR"),"/mariokart.rda"))
m<-(lm(total_pr~cond+stock_photo+duration+wheels,data=mariokart))
summary(m)
Call:
lm(formula = total_pr ~ cond + stock_photo + duration + wheels,
data = mariokart)
Residuals:
Min 1Q Median 3Q Max
-19.485 -6.511 -2.530 1.836 263.025
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 43.5201 8.3701 5.199 7.05e-07 ***
condused -2.5816 5.2272 -0.494 0.622183
stock_photoyes -6.7542 5.1729 -1.306 0.193836
duration 0.3788 0.9388 0.403 0.687206
wheels 9.9476 2.7184 3.659 0.000359 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 24.4 on 138 degrees of freedom
Multiple R-squared: 0.1235, Adjusted R-squared: 0.09808
F-statistic: 4.86 on 4 and 138 DF, p-value: 0.001069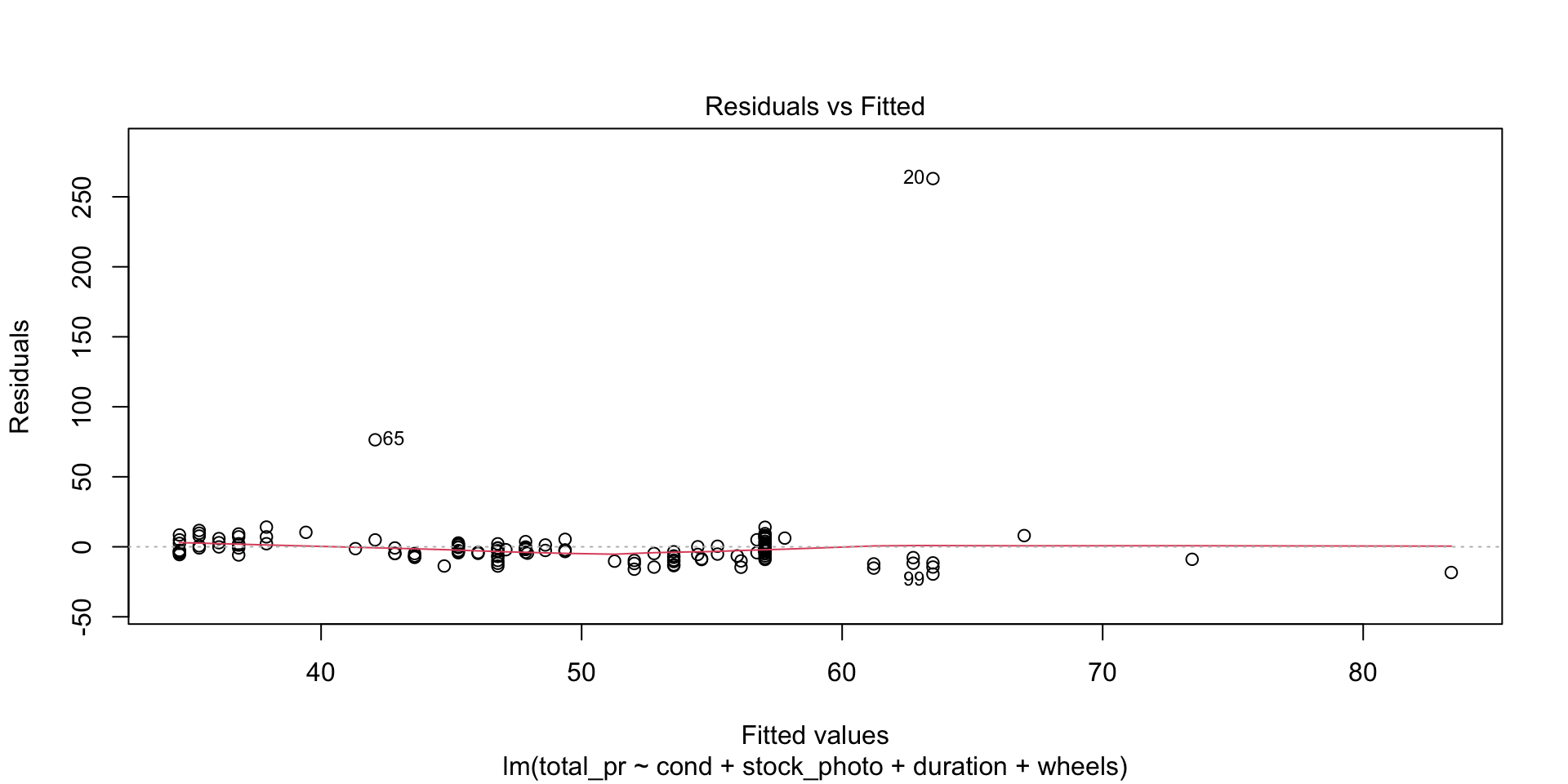
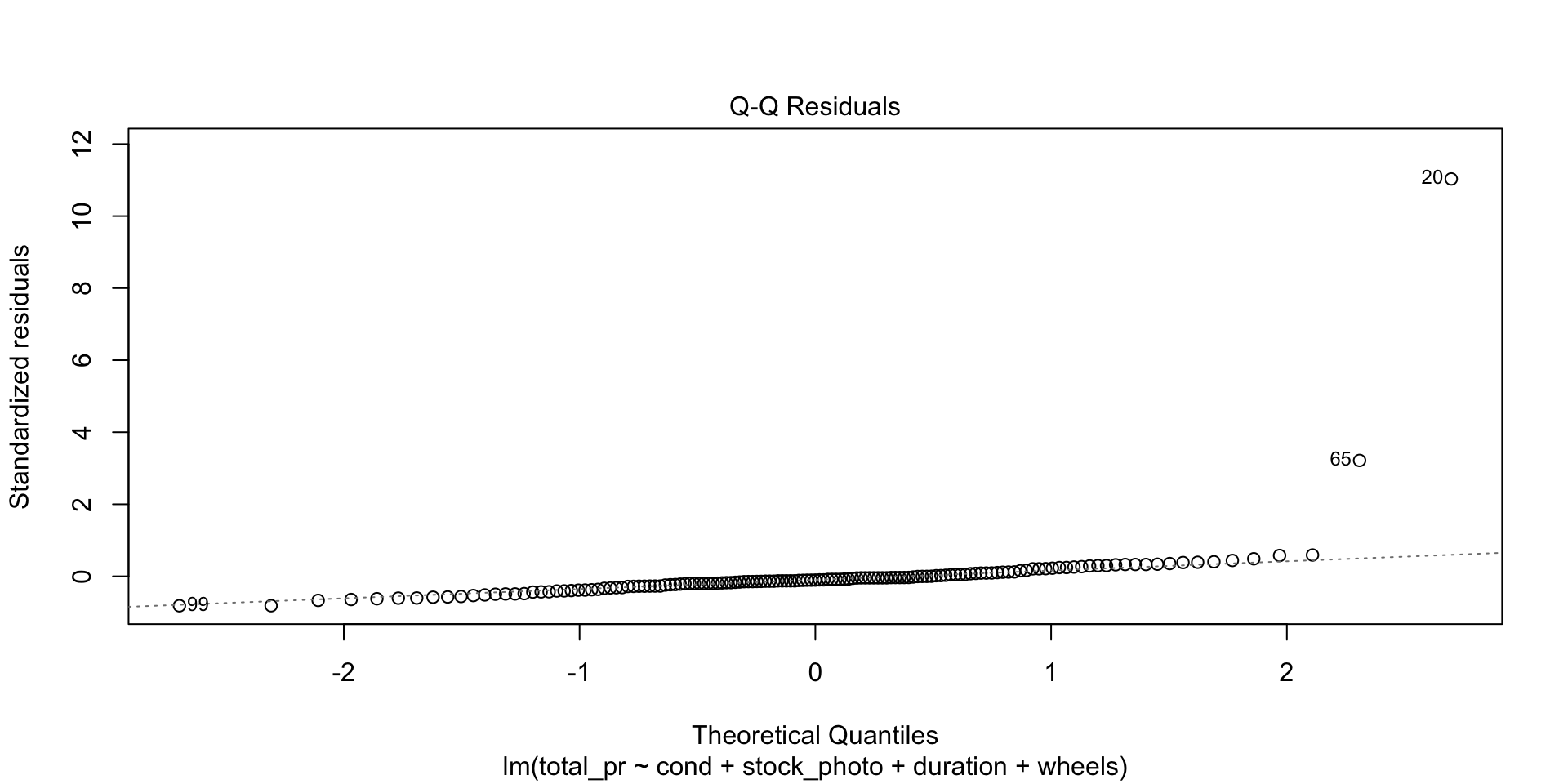
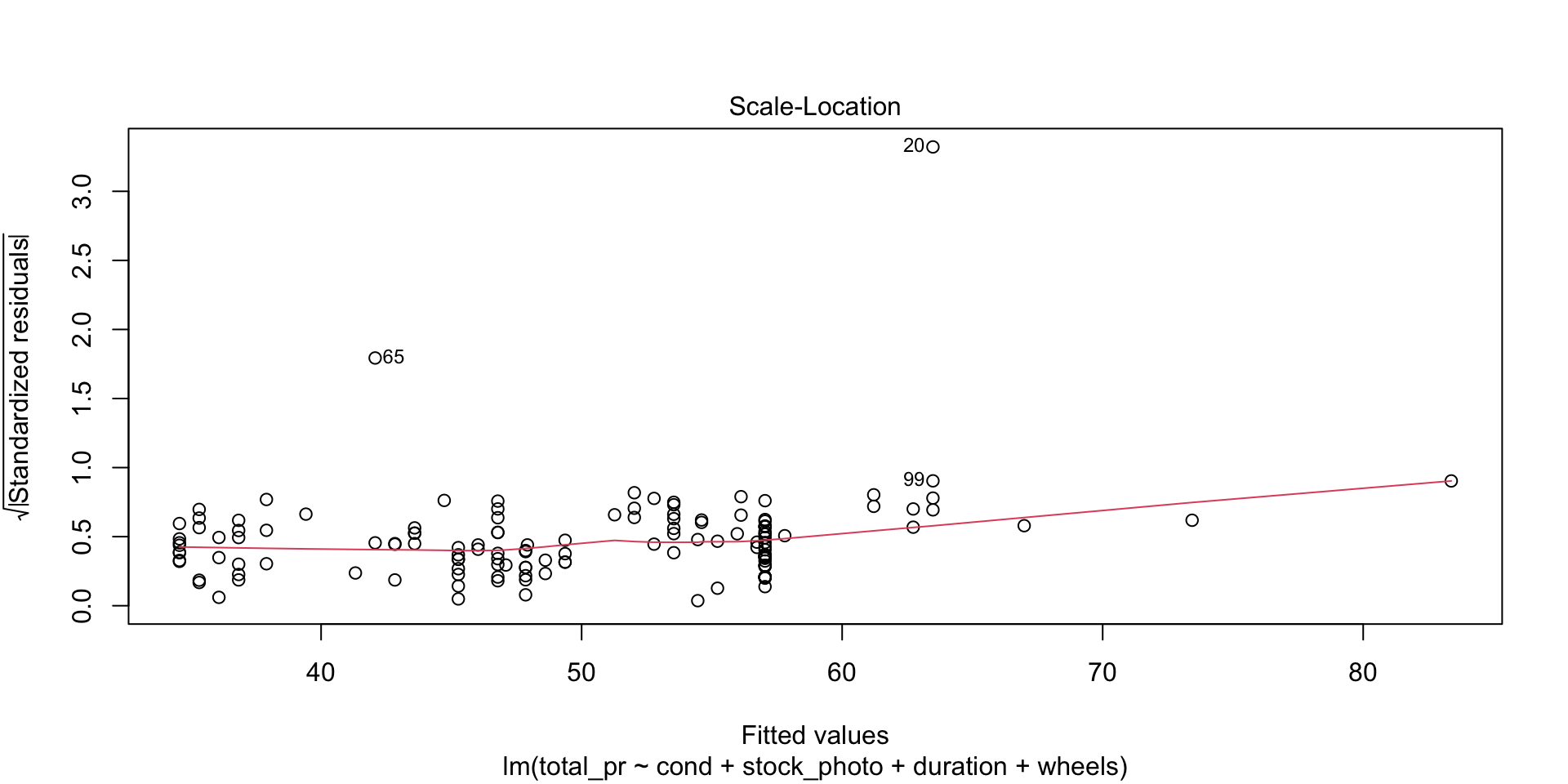
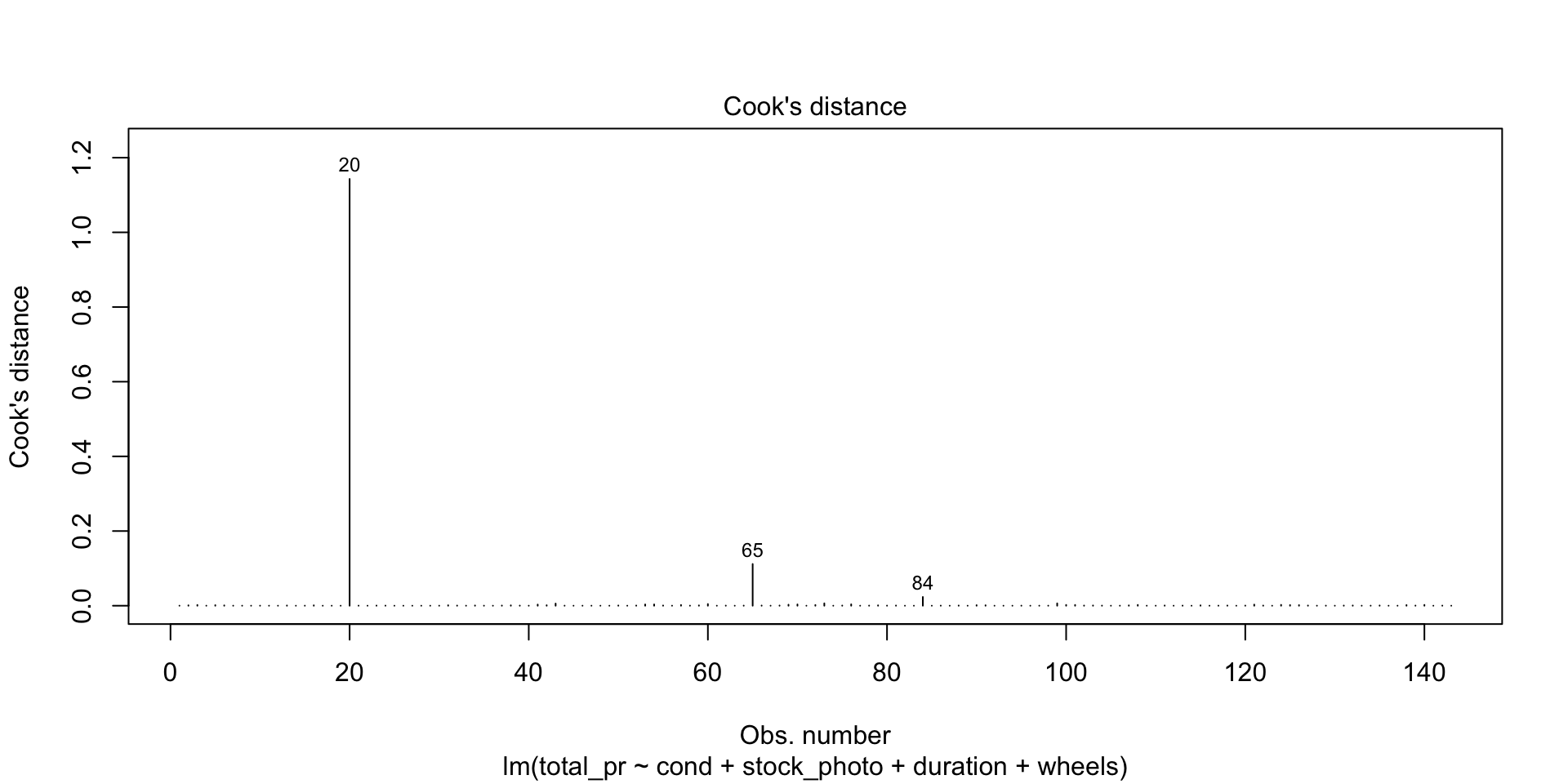
There are four diagnostic plots in the above output. Each one gives us information about the quality of the model.
Residuals vs Fitted
This plot tells you the magnitude of the difference between the residuals and the fitted values. There are three things to watch for here. First, are there any drastic outliers? Yes, there are two, points 65 and 20. (Those are row numbers in the data frame.) You need to investigate those and decide whether to omit them from further analysis. Were they typos? Mismeasurements? Or is the process from which they derive intrinsically subject to occasional extreme variation. In the third case, you probably don’t want to omit them.
Second, is the solid red line near the dashed zero line? Yes it is, indicating that the residuals have a mean of approximately zero. (The red line shows the mean of the residuals in the immediate region of the \(x\)-values of the observed data.)
Third, is there a pattern to the residuals? No, there is not. The residuals appear to be of the same general magnitude at one end as the other. The things that would need action would be a curve or multiple curves, or a widening or narrowing shape, like the cross section of a horn.
Normal Q-Q
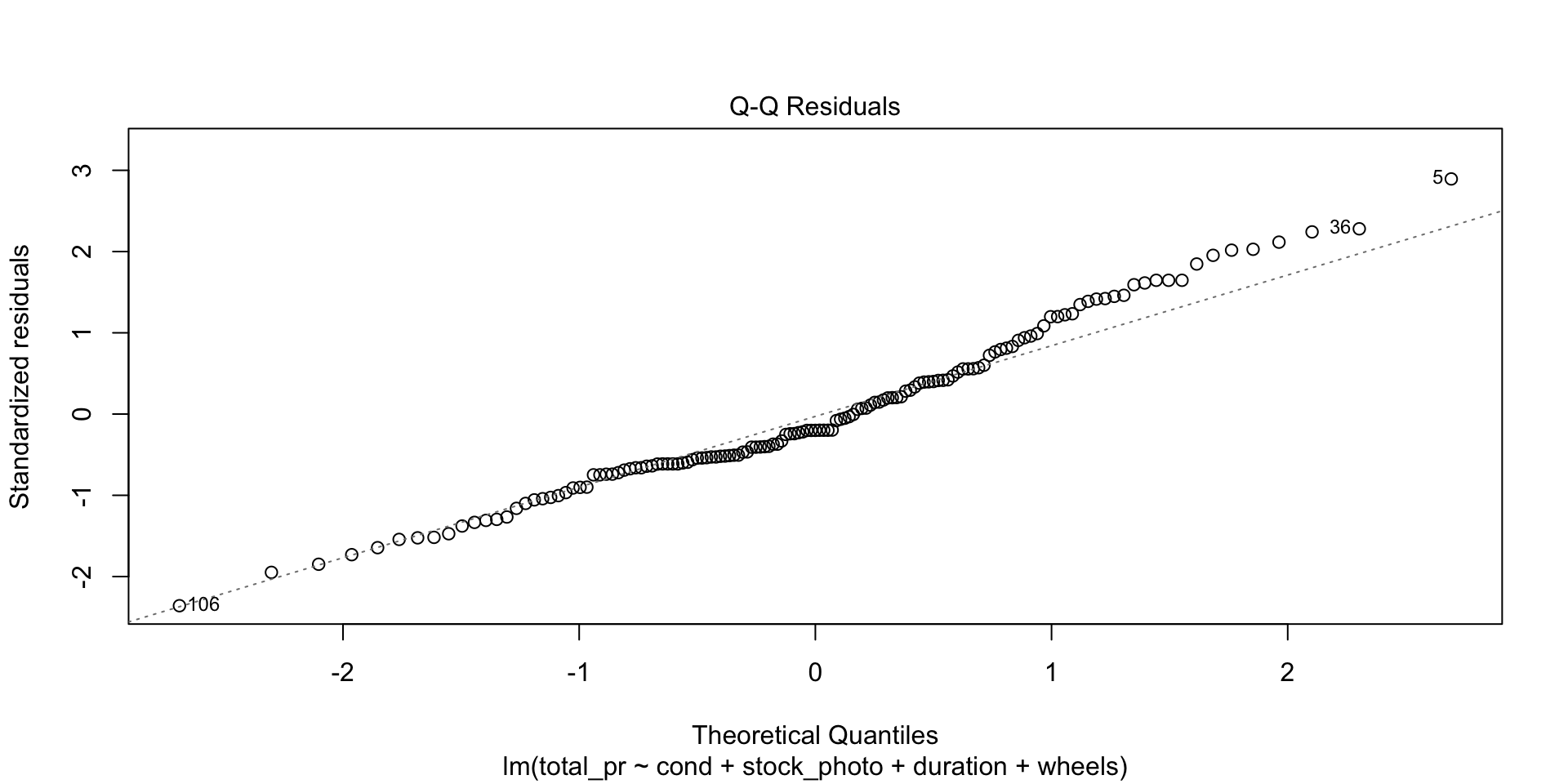
This is an important plot. I see many students erroneously claiming that residuals are normally distributed because they have a vague bell shape. That is not good enough to detect normality. The Q-Q plot is the standard way to detect normality. If the points lie along the dashed line, you can be reasonably safe in an assumption of normality. If they deviate from the dashed line, the residuals are probably not normally distributed.
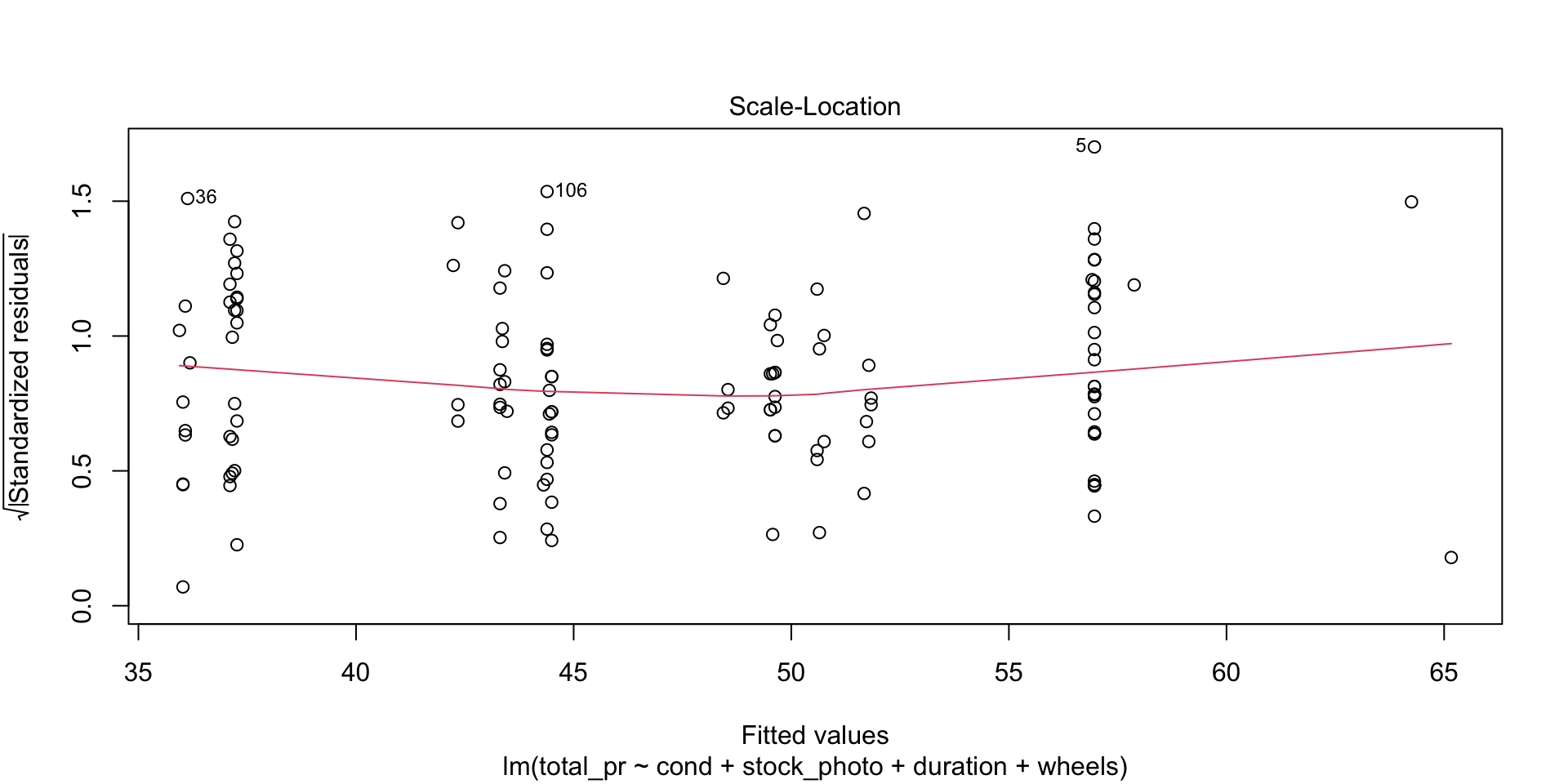
Scale-Location
Look for two things here. First, the red line should be approximately horizontal, meaning that there is not much variability in the standardized residuals. Second, look at the spread of the points around the red line. If they don’t show a pattrn, this reinforces the assumption of homoscedasticity that we already found evidence for in the first plot.
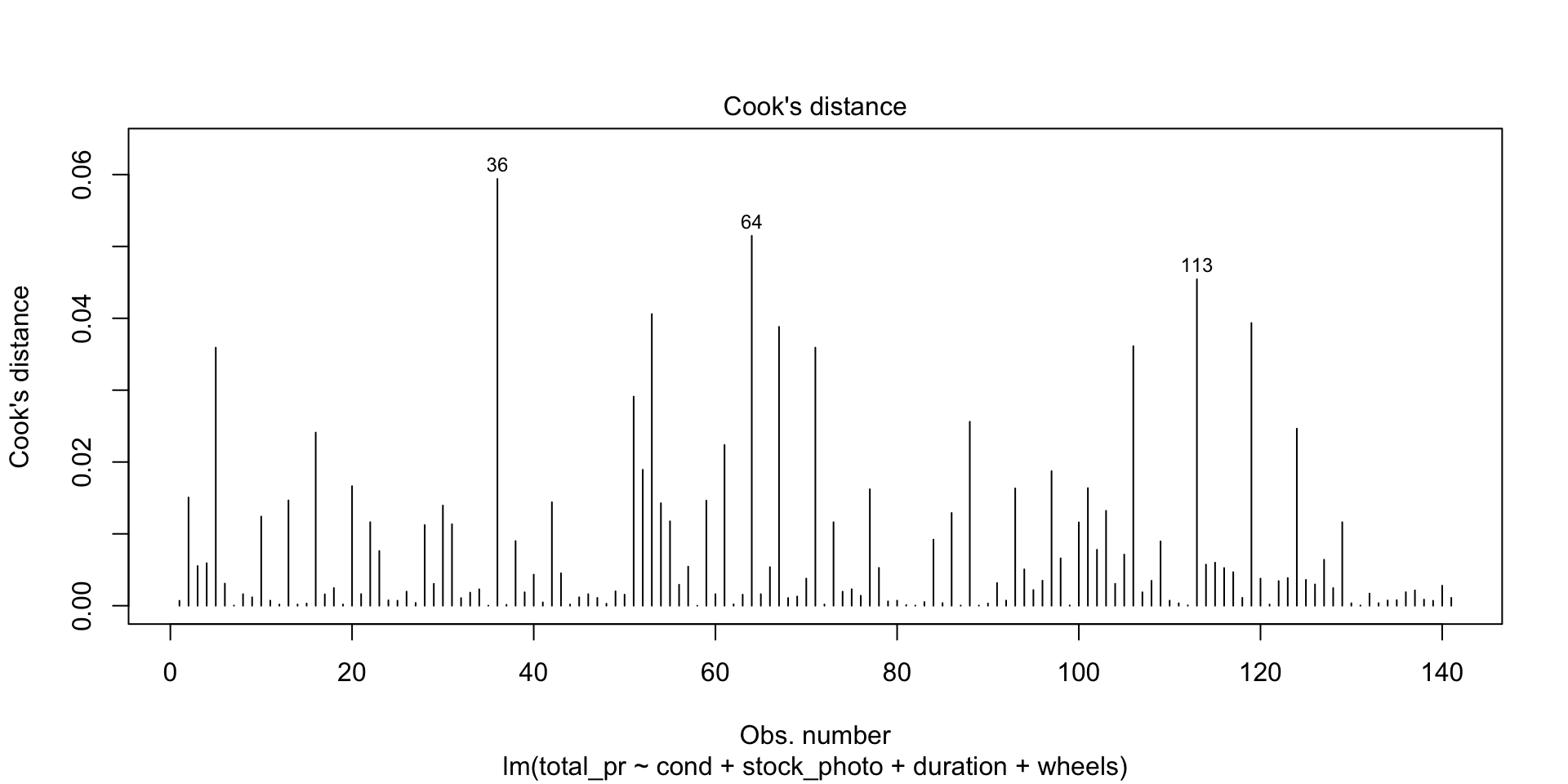
Residuals vs Leverage
This shows you influential points that you may want to remove. Point 84 has high leverage (potential for influence) but is probably not actually very influential because it is so far from Cook’s Distance. Points 20 and 65 are outliers but only point 20 is more than Cook’s Distance away from the mean. In this case, you would likely remove point 20 from consideration unless there were a mitigating reason. For example, game collectors often pay extra for a game that has unusual attributes, such as shrink-wrapped original edition.
As an example of a point you would definitely remove, draw a horizontal line from point 20 to a vertical line from point 84. Where they meet would be a high-leverage outlier that is unduly affecting the model no matter what it’s underlying cause. On the other hand, what if you have many such points? Unfortunately, that probably means the model isn’t very good.
Removing offending observations
Suppose we want to get rid of points 20 and 65 and rerun the regression. We could either do this using plain R or the tidyverse. I prefer the tidyverse method because of clarity of exposition.
df <- mariokart |>
filter(!row_number() %in% c(20, 65))
m<-(lm(total_pr~cond+stock_photo+duration+wheels,data=df))
summary(m)
Call:
lm(formula = total_pr ~ cond + stock_photo + duration + wheels,
data = df)
Residuals:
Min 1Q Median 3Q Max
-11.3788 -2.9854 -0.9654 2.6915 14.0346
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 41.34153 1.71167 24.153 < 2e-16 ***
condused -5.13056 1.05112 -4.881 2.91e-06 ***
stock_photoyes 1.08031 1.05682 1.022 0.308
duration -0.02681 0.19041 -0.141 0.888
wheels 7.28518 0.55469 13.134 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.901 on 136 degrees of freedom
Multiple R-squared: 0.719, Adjusted R-squared: 0.7108
F-statistic: 87.01 on 4 and 136 DF, p-value: < 2.2e-16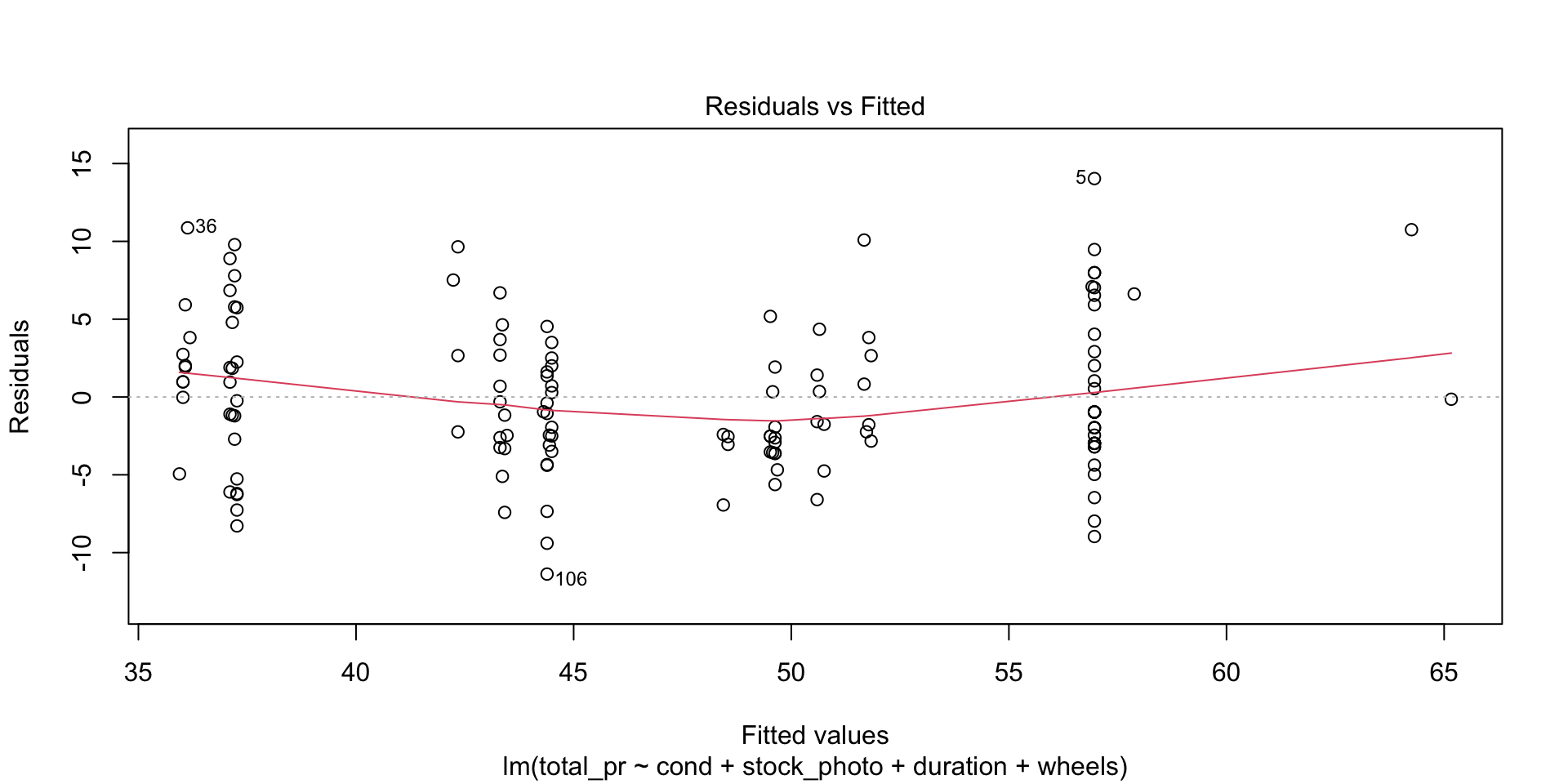
What a difference this makes in the output and the statistics and plots about the output! Keep in mind, though, that I just did this as an example. Points 20 and 65 may be totally legitimate in this case. Also, note that you could use plain R without the tidyverse to eliminate those rows by saying something like df <- mariokart[-c(20,65),]. The bracket notation assumes anything before the comma refers to a row and anything after a comma refers to a column. In this case, I didn’t say anything about the columns, so the square brackets just have a dangling comma in them. The important point is that one method or another may seem more natural to you. For most students, the tidyverse approach is probably more natural, so I highlight that.
Regression gone wrong
There is a dataframe in both the MASS and ISLR2 called Boston. It illustrates the problem of systemic racism and how that can affect statistical models such as we are generating in logistic regression. It is instructive to look at this dataframe rather than ignore it so we can learn how such things happen and, perhaps, how to guard against them.
The Boston dataframe is popular in textbooks and statistics classes. I’ve used it myself without thinking too much about it. It has a column called black which I naively assumed could be used to illustrate racism in Boston, a city notorious for segregation of the black population into a ghetto.
I was about to use it in this class when a student asked if the black column was removed in the ISLR2 package because of racism. I didn’t know. I looked at both copies, the one in MASS and the one in ISLR2 (a more recent package) and discovered that, indeed, the black column had been removed in the more recent package. Why? I searched for articles about the Boston dataframe and found two alarming articles analyzing it, one of which pointed out that some prominent statisticians had deleted it from their Python package after learning of the problem.
Far from being used to illustrate racism, this dataframe may have actually been perpetuating racist activity. The original purpose of the dataframe is innocuous. It is meant to illustrate the relationship of air pollution to housing prices, which seems like a laudable goal. There is evidence, though, that in assembling the dataframe, the creators made some racist assumptions that have had a lasting negative effect. What we know about assembling the dataframe is incomplete, based on incomplete documentation and attempted reconstruction by M. Carlisle, a self-described Mathematics PhD posting on Medium. The following information comes from Carlisle’s post, although I am responsible for any errors of interpretation.
It appears that the creators of the dataframe committed an error you can easily avoid, thanks in part to contemporary tools that were not available in 1975. They took some data from the US Census, but did not record it directly. Instead, they subjected it to a non-invertible transformation and recorded the result. That means that we can’t be sure of the original data and we are stuck, in a sense, with their interpretation of that data.
Critically, that interpretation encoded two racist assumptions that should have been testable to root out racism rather than encoded to perpetuate it. The transformation is \(v=1000(B-0.63)^2\), where \(B\) is the proportion of the Black population by town. By non-invertible it is meant that \(B\) can’t be derived from \(v\) except in some cases because squaring makes the number positive regardless of whether \(B-0.63\) is positive or negative. This is a very basic error you should not emulate. Luckily, tools like Quarto make it possible to document all your transformations so you can use the raw data and someone else can substitute a different transformation. This is a key point to remember.
What about the equation itself? What social value is it encoding? Keep in mind that \(v\) is the contribution of “Blackness” to the median value of homes in a town. The shape of the function is a parabola as follows.
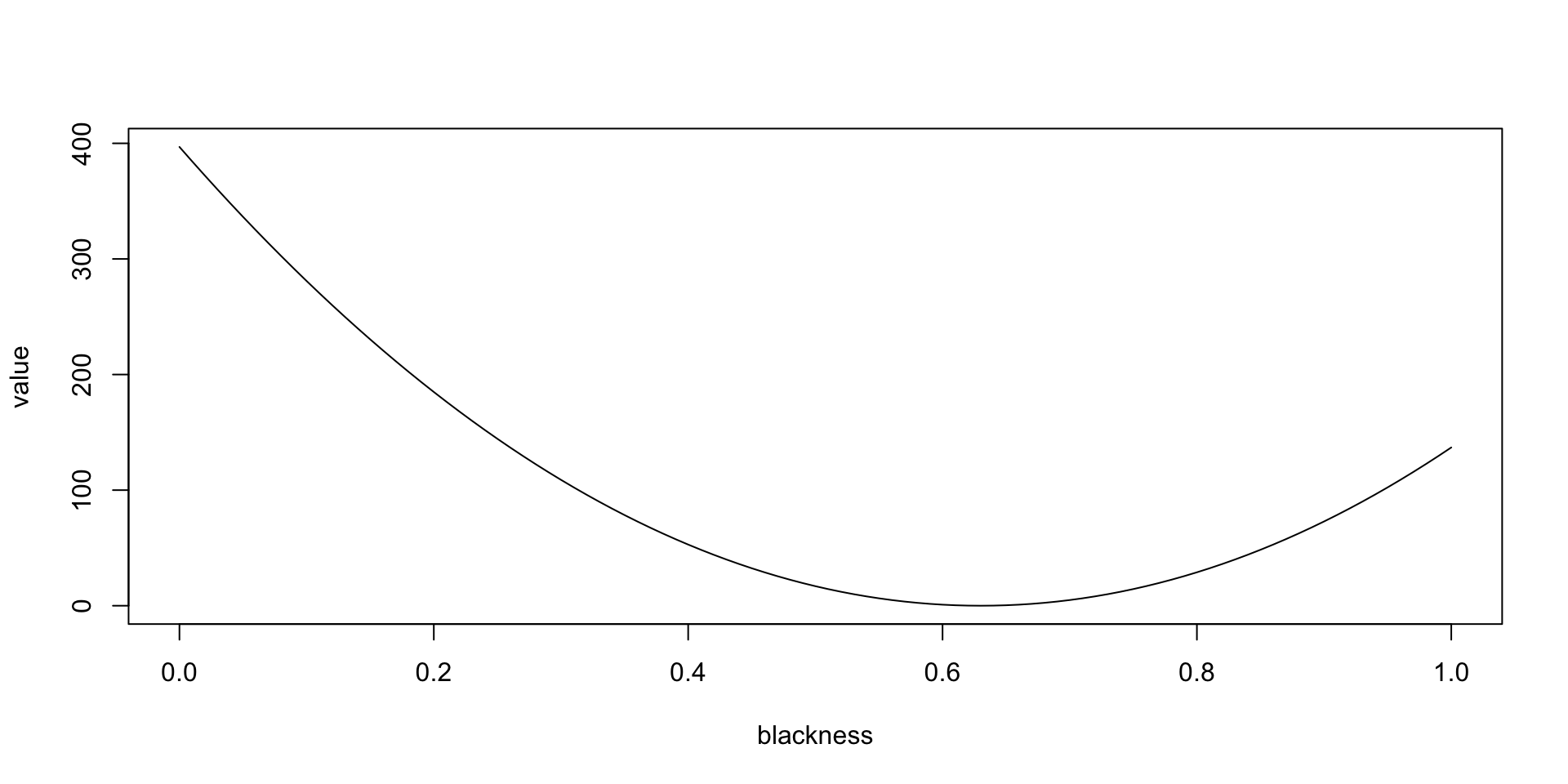
It appears that the value is in squared thousands of dollars, meaning that the median value of a totally segregated white neighborhood is about 19.9223493K USD higher than that of a neighborhood with 63 percent black population (where the parabola bottoms out). In a completely black neighborhood, the median value of a home is about 11.7004273K USD more than in the neighborhood with 63 percent black population. In other words, the equation is telling current homeowners that the value of their home will be decreased by integration and that they are financially better off under segregation.
What if this dataframe is used for inferring the appropriate sale price of new homes? This is really pernicious. It helps to perpetuate segregation by reinforcing the parabola. The fact that that this has become a textbook dataframe practically ensures that someone will use it to set prices or to make offers.
When M. Carlisle set out to find out the original Census numbers used, it turned out to be impossible, presumably because of sloppiness in the original data collection. As you may guess, there are only two possibilities for \(v\) for every instance of \(B\), so some matching should be possible. But it wasn’t possible for every town! The numbers from the analysis didn’t match any numbers from the 1970 census in several cases.
There is another glaring problem with this dataframe, mentioned in the other article I found, at FairLearn. That article includes the following paragraph:
The definition of the LSTAT variable is also suspect. Harrison and Rubenfield define lower status as a function of the proportion of adults without some high school education and the proportion of male workers classified as laborers. They apply a logarithmic transformation to the variable with the assumption that resulting variable distribution reflects their understanding of socioeconomic distinctions. However, the categorization of a certain level of education and job category as indicative of “lower status” is reflective of social constructs of class and not objective fact. Again, the authors provide no evidence of a proposed relationship between LSTAT and MEDV and do not sufficiently justify its inclusion in the hedonic pricing model.
The lstat column is problematic for at least three reasons: (1) it represents a hypothesis with no empirical support, (2) it exhibits intersectionality with the black column because of the prevalance of black males in both categories, and (3) it is a jumble of three things (education, job classification, and logarithmic transformation) meant to reinforce a social conception of “class”. Contemporary toolkits like Quarto can partially ameliorate problems like (3) by keeping an audit trail from raw data through model building. But (1) requires you to drop stereotypes rather than turn them into unsupported hypotheses and (2) challenges you to more deeply understand data to spot potential for malfeasance.
What about other ethical problems with this dataframe? The FairLearn article goes into more depth than I have here and unpacks the problems into different named constructs with precise definitions. It is well worth reading. It also references the discussion over what to do with this dataframe on GitHub. You can see evidence of what some people chose to do by comparing the MASS and ISLR2 versions, both of which are mistaken in their disposition in my opinion. Ultimately, the FairLearn article recommends abandoning this dataframe for predictive analysis exercises, so I have done that in our weekly exercises. Special thanks are owed to the student who got me searching for the above information!
Logistic Regression
Logistic Regression Intro
Logistic regression is a kind of classification rather than regression. The book doesn’t make this point, but most textbooks do. You can divide machine learning problems into problems of regression and problems of classification. In regression, the \(y\) variable is more or less continuous, whereas in the classification problem, \(y\) is a set of categories, ordered or not. The word logistic comes from the logistic function, which is illustrated below. This interesting function takes an input from \(-\infty\) to \(+\infty\) and gives an output between zero and one. It can be used to reduce wildly varying inputs into a yes / no decision. It is also known as the sigmoid function.
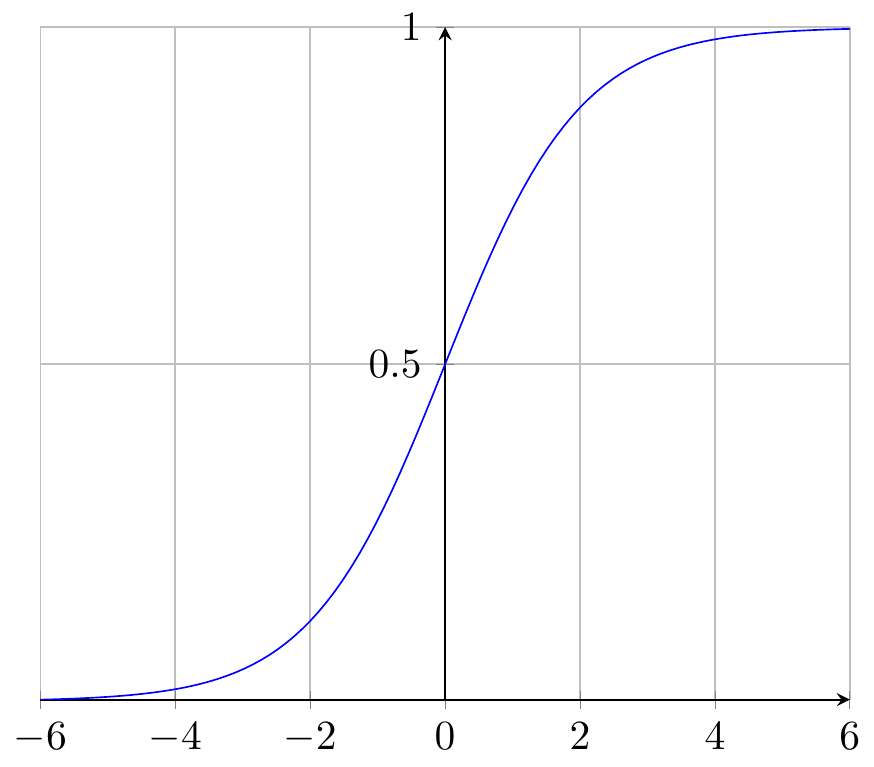
Note that zero and one happen to be the boundaries of a probability measure. Hence, you can use the logistic function to reduce arbitrary numbers to a probability.
[1] "job_ad_id" "job_city" "job_industry"
[4] "job_type" "job_fed_contractor" "job_equal_opp_employer"
[7] "job_ownership" "job_req_any" "job_req_communication"
[10] "job_req_education" "job_req_min_experience" "job_req_computer"
[13] "job_req_organization" "job_req_school" "received_callback"
[16] "firstname" "race" "gender"
[19] "years_college" "college_degree" "honors"
[22] "worked_during_school" "years_experience" "computer_skills"
[25] "special_skills" "volunteer" "military"
[28] "employment_holes" "has_email_address" "resume_quality"
Call:
glm(formula = received_callback ~ honors, family = "binomial",
data = resume)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.4998 0.0556 -44.96 < 2e-16 ***
honors 0.8668 0.1776 4.88 1.06e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2726.9 on 4869 degrees of freedom
Residual deviance: 2706.7 on 4868 degrees of freedom
AIC: 2710.7
Number of Fisher Scoring iterations: 5
Call:
glm(formula = received_callback ~ race, family = "binomial",
data = resume)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.67481 0.08251 -32.417 < 2e-16 ***
racewhite 0.43818 0.10732 4.083 4.45e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2726.9 on 4869 degrees of freedom
Residual deviance: 2709.9 on 4868 degrees of freedom
AIC: 2713.9
Number of Fisher Scoring iterations: 5
Call:
glm(formula = received_callback ~ gender, family = "binomial",
data = resume)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.40901 0.05939 -40.562 <2e-16 ***
genderm -0.12008 0.12859 -0.934 0.35
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2726.9 on 4869 degrees of freedom
Residual deviance: 2726.0 on 4868 degrees of freedom
AIC: 2730
Number of Fisher Scoring iterations: 5One easy way to compare these models is by comparing the values of AIC, the Akaike Information Criterion. This measures the loss of information in each model and the model with the lowest value of AIC has lost the least. In comparing the AIC values, it is typical to calculate \(\exp((\text{AIC}_{\text{min}}-\text{AIC}_{\text{alternative}})/2)\). This value, the relative likelihood, is the likelihood that the alternative model minimizes the information loss.
Keep in mind that the AIC is only a tool to compare models, not an absolute measure. There is no such thing as an absolutely good AIC value. In the above cases, the relative likelihood for the two models with higher AIC values is vanishingly small. The model using honors loses far less information than do the other two.
Another approach is to calculate AICc, Delta_AICc, and AICcWt using R.
m1 <- glm(received_callback ~ honors,data=resume,family="binomial")
m2 <- glm(received_callback ~ race,data=resume,family="binomial")
m3 <- glm(received_callback ~ gender,data=resume,family="binomial")
pacman::p_load(AICcmodavg)
models <- list(m1,m2,m3)
model_names <- c("honors", "race", "gender")
aictab(cand.set = models, modnames = model_names)
Model selection based on AICc:
K AICc Delta_AICc AICcWt Cum.Wt LL
honors 2 2710.73 0.00 0.83 0.83 -1353.36
race 2 2713.94 3.21 0.17 1.00 -1354.97
gender 2 2730.03 19.31 0.00 1.00 -1363.02A common rule, discredited by Anderson (2008) is that, if Delta_AICc is greater than 2, the model should be discarded. But it is not the case that any model can be judged as good or bad based on AIC. Instead, the AIC tells us only relative information about the models: which is better from an information loss standpoint. The AICcWt or Akaike weight, is the probability that the given model is the best of the models in the table from an information loss standpoint. Here there is a clear winner. The difference between 83 percent and seventeen percent is striking.
tidymodels approach
Datacamp shows a different way, using tidymodels in one of their tutorials. In this example, the bank wants to divide customers into those likely to buy and those unlikely to buy some banking product. They would like to divide the customers into these two groups using logistic regression, with a cutoff point of fifty-fifty. If there’s better than a fifty-fifty chance, they will send a salesperson but if there’s less than a fifty-fifty chance, they won’t send a salesperson.
pacman::p_load(tidymodels)
#. Read the dataset and convert the target variable to a factor
bank_df <- read_csv2(paste0(Sys.getenv("STATS_DATA_DIR"),"/bank-full.csv"))
bank_df$y = as.factor(bank_df$y)
#. Plot job occupation against the target variable
ggplot(bank_df, aes(job, fill = y)) +
geom_bar() +
coord_flip()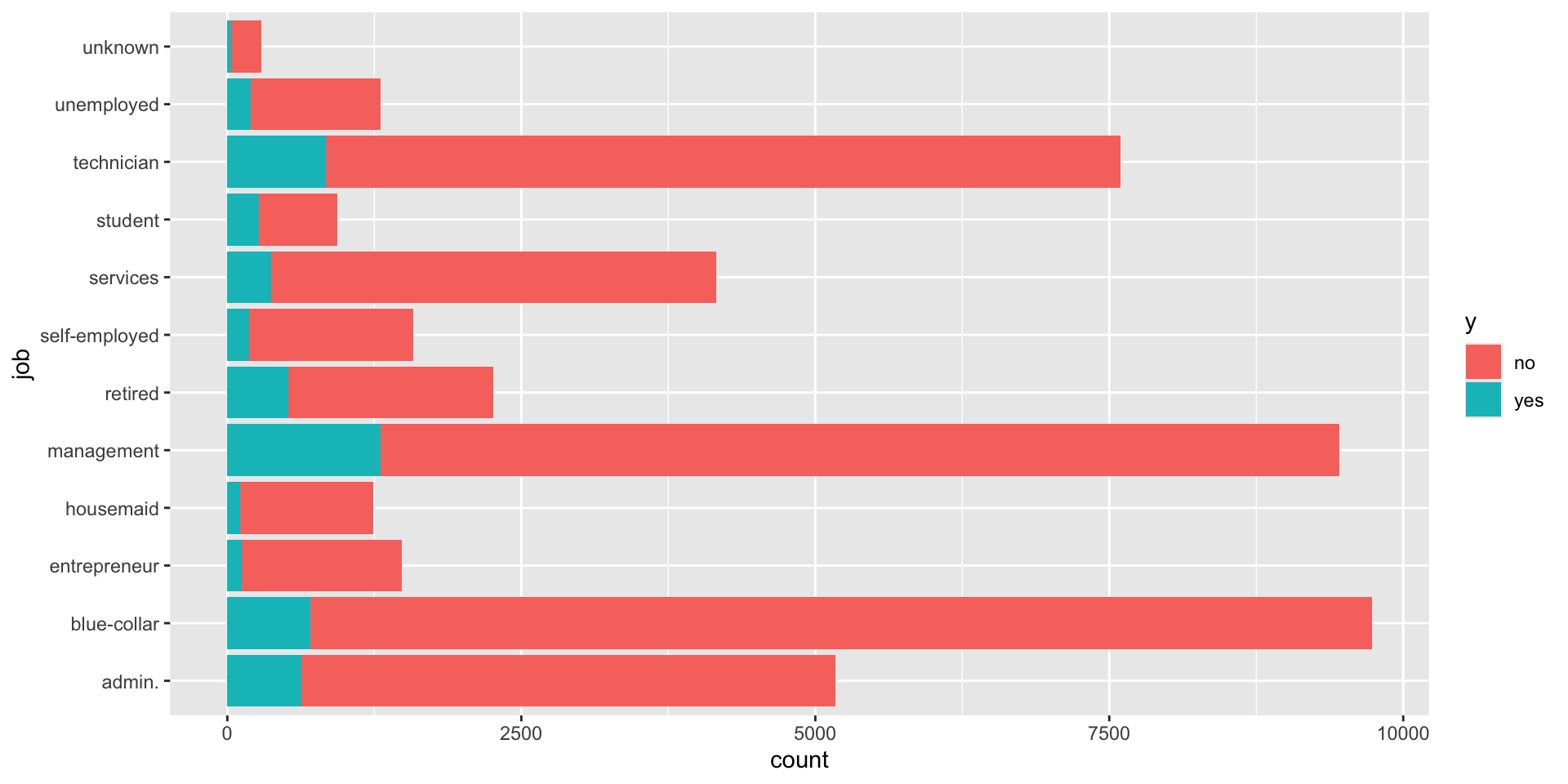
A crucial concept you’ll learn if you take a more advanced class, say 310D, is the notion of dividing data into two or three data frames, a training frame, a validation frame and a test frame. This is the conventional way to test machine learning models, of which logistic regression is one. You train the model on one set of data, validate it on another, then test it on another, previously unseen set. The next thing in this example is training and testing.
# A tibble: 43 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) -2.59 0
2 age -0.000477 0
3 jobblue-collar -0.183 0
4 jobentrepreneur -0.206 0
5 jobhousemaid -0.270 0
6 jobmanagement -0.0190 0
7 jobretired 0.360 0
8 jobself-employed -0.101 0
9 jobservices -0.105 0
10 jobstudent 0.415 0
# ℹ 33 more rowsHyperparameter tuning
There are aspects of this approach, called hyperparameters, that influence the quality of the model. It can be tedious to adjust these aspects, called penalty and mixture, so here’s a technique for doing it automatically. You’ll learn about this and similar techniques if you take a more advanced course like 310D, Intro to Data Science.
Truth
Prediction no yes
no 7838 738
yes 147 320# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 precision binary 0.914# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 recall binary 0.982Evaluation metrics
Following are two tables from James et al. (2021) that you can use to evaluate a classification model.
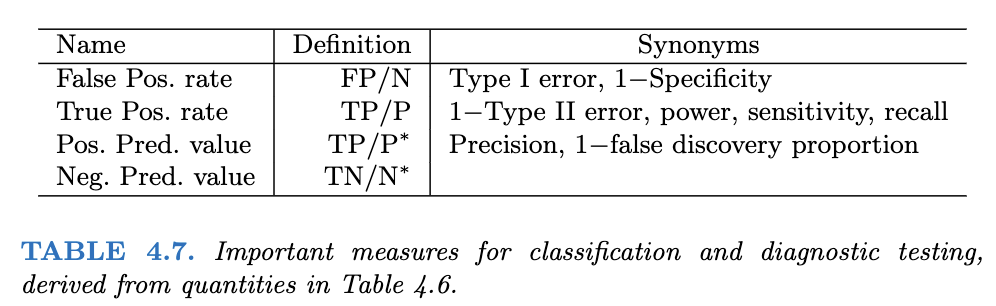
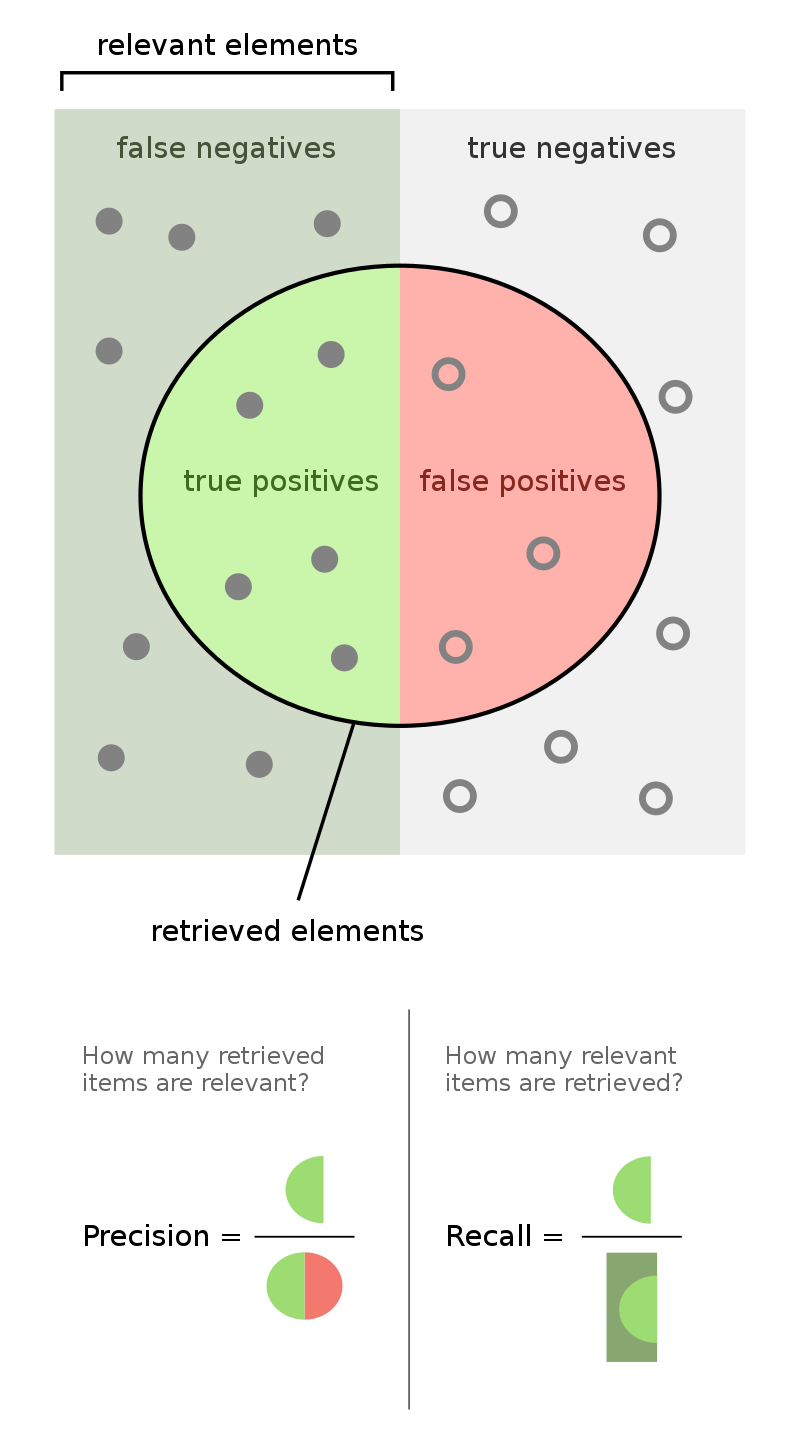
Another view is provided at Wikipedia in the following picture
# A tibble: 10 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) -2.59 0.0000000001
2 poutcomesuccess 2.08 0.0000000001
3 monthmar 1.62 0.0000000001
4 monthoct 1.08 0.0000000001
5 monthsep 1.03 0.0000000001
6 contactunknown -1.01 0.0000000001
7 monthdec 0.861 0.0000000001
8 monthjan -0.820 0.0000000001
9 housingyes -0.550 0.0000000001
10 monthnov -0.517 0.0000000001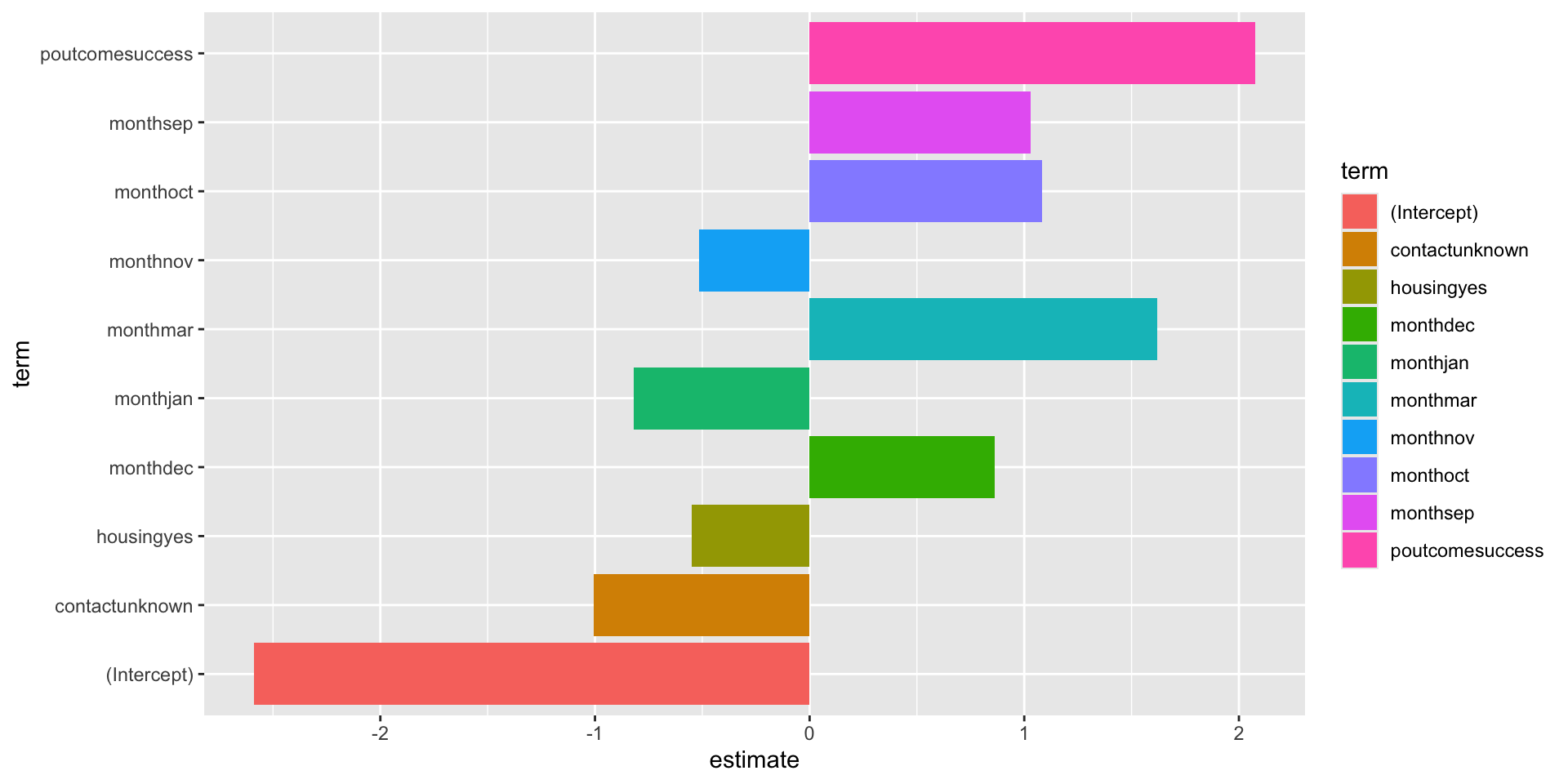
References
Colophon
This slideshow was produced using quarto
Fonts are Roboto Condensed Bold, JetBrains Mono Nerd Font, and STIX2